Cuestionario sobre Infinitos

1) ¿Cuántas variedades de infinitos distinguió Aristóteles?
2) ¿Cómo se llama el tipo de infinito que desarrolló el matemático George Cantor ?
3) ¿Es un infinito contable el conjunto de los números racionales?
4) Encuentra un ejemplo de un infinito no contable.
5) ¿Cuáles fueron las consecuencias del nuevo concepto de infinito introducido por Cantor? ¿Fueron aceptadas sus ideas ?
6) Nombrar otros tipos de infinitos que no sean los infinitos matemáticos.

Recomendamos ver el siguiente video sobre el Infinito:

http://www.eitb.tv/es/video/naukas--bilbao/2698453634001/2705799411001/miguel-a-morales-gaussianos/

Actividades-La divina proporcion

ACTIVIDADES  Trabajamos con el numero de oro

Luego de leer los documentos  The  Divine Proportion y Phi, Pi and the Great Pyramid of Egypt at Giza realiza las siguientes propuestas:

Primera aproximación al número de oro…

1.   Se elegirá un voluntario para pasar al frente.

2.   Se harán las siguientes mediciones, registrándolas en el pizarrón:

(A)   distancia del hombro a los dedos

(B)   distancia del codo a los dedos

(C)   distancia entre el hombro y el codo.

3.   Se propondrán las siguientes razones:

                     A=B

                   B  C

4.   Se procederá de la misma manera con varios compañeros.

5.   Se sacarán conclusiones.

6. Vuelve a leer atentamente el documento  Phi, Pi and the Great Pyramid of Egypt at Giza y en carton construye en verdadera magnitud tu propia piramide para las mismas proporciones que la Gran Piramide.

Video animado sobre la Proporción aurea

 

THE DIVINE PROPORTION

Geometry has two great treasures; one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold, the second we may name a precious jewel.
--Johannes Kepler

In a paragraph towards the end of his 1611 essay On the Six Cornered Snowflake Kepler mentions the “Divine Proportion" (Golden section) and the "fibonacci sequence” in practically the same breath as flowers and pentagons. "It is in the likeness of this self-developing series that the faculty of propagation is, in my opinion, manifest: and so in a flower the authentic flag of this faculty is shown, the pentagon." (emphasis added)

What does Kepler mean here?

First, we examine the nature of the logarithmic spiral, for reasons that will become evident below.

The 17th century mathematician Jakob Bernoulli named the figure at right the Spira mirabilis or "miraculous spiral" and assigned it the following motto: "Eadem mutato resurgo" ("although changed, I rise again the same"). The logarithmic spiral does not change its shape as its size increases. This feature is known as self-similarity. If we could zoom into the coils of the figure near the origin    and enlarge them, they would fit precisely on the larger spiral. The spiral has another extraordinary property: turning by equal angles increases the distance from the pole to the spiral by equal ratios.

What are fibonacci numbers?

 

In the "fibonacci sequence," referenced by Kepler, each number is the sum of the two proceeding numbers (1, 2, 3, 5, 8, 13, 21...). Therefore, the sequence can be called a "self-developing" series.

Interestingly, dividing two adjacent fibonacci number (8/5 or 21/13, for example) by each other produces increasingly precise approximation of the "Divine Proportion," which we will explore below, as the numbers grow larger.

Why does Kepler mention flowers? Scientists, beginning with Leonardo da Vinci, observed that the displacement of leaves around a stem occurs in patterns defined by the fibonacci series. This phenomenon is known as "philotaxis." In the case of roses an angle that is congruent to 360 degrees by the Divine Proportion (137.5 degrees) separates the petals from each other.

 

In other plants the number of leaves measured around a screw-type displacement between one leaf and the leaf directly above it, and the number of rows separating the two are both fibonacci numbers. The same phenomenon occurs in pinecones and the hearts of sunflowers.

How is the Divine Proportion related to the pentagon?

The Divine Proportion plays an essential role in the construction of the pentagon and five-fold symmetry.

To see this, examine the diagonals in a pentagon. The ratio of the diagonal to the side of a pentagon is the Divine Proportion. Moreover, the diagonals create an isosceles triangle (where two of the three sides are equal) with angles of 72 degrees and 36 degrees. This triangle can be reproduced inside itself to infinity (in a "self-developing" manner), as shown below.

                           

                            

 

In constructions of tiled pentagons, every segment is smaller than its predecessor by a factor equal to the Divine Proportion.

 

(the ratio of "a" to "b" is the Divine Proportion, the ratio of "b" to "c" is the Divine Proportion, and so on.

How does this relate to the logarithmic spiral?

In a rectangle where the ratio of the larger side to the smaller one is the Divine Proportion, the ratio of the sides of the "daughter rectangles" will still conform to the Divine Proportion when squares are cut from the original rectangle. Connecting the points where this series of "whirling squares" divides the sides will generate a logarithmic spiral that coils inward.

Similarly, connecting the vertices of the nested "Golden Triangles" inside the pentagon will produce the logarithmic spiral as well.

What is the "extreme and mean ratio?"

Euclid defines the "extreme and mean ratio," or "Divine Proportion," as the following relationship: When a line is divided such that the smaller section of the line (BC) is related to the larger section of the line (AC) in the same ratio as the larger section is related to the whole line (AC), then the line is divided in the Divine Proportion.

 

                      

 

The search for harmonic relationships in the natural world motivated Kepler's scientific investigations. Whether endeavoring to understand the structure of snowflakes and or seeking the principles that underlie the organization of the cosmos as a whole, Kepler saw congruencies in nature and between the human intellect and the material world as evidence of the goodness of God and signposts of man's divine potential.

Kepler wrote, "For the theater of the world is so ordered that there exist in it suitable signs by which human minds, likenesses of God, are not only invited to study the divine works, from which they may evaluate the founder's goodness, but are also assisted in inquiring more deeply." (Optics, p. 15)

Kepler's ideas about harmony, proportion, and the nature of knowledge can be more fully appreciated with reference to the work of the renaissance statesman and mathematician, Cardinal Nicholas of Cusa (1401-1464), whose influence may be glimpsed throughout the astronomer's work.

 

 

En  http://www.keplersdiscovery.com/SixCornered.html  puedes ver el documento completo.

Otros documentos donde ampliar la informacion

http://tympanus.net/codrops/2012/04/17/the-divine-proportion-and-web-design/

http://www.goldennumber.net/human-body/

 

 

 

Phi, Pi and the
  

Great Pyramid of Egypt at Giza

---

The Great Pyramid of Egypt is based on Golden Ratio proportions

There is still some debate as to whether the Great Pyramid of Giza in Egypt, built around 2560 BC, was constructed with dimensions based on phi, the golden ratio.  Its once flat, smooth outer shell is gone and all that remains is the roughly-shaped inner core, so it is difficult to know with certainty.
There is compelling evidence, however, that the design of the pyramid embodied these foundations of mathematics and geometry:

• Phi, the Golden Ratio that appears throughout nature.
• Pi, the circumference of a circle in relation to its diameter.
• The Pythagorean Theorem – Credited by tradition to mathematician Pythagoras (about 570 – 495 BC), which can be expressed as a² + b² = c².

First, phi is the only number which has the mathematical property of its square being one more than itself:

 Φ + 1 = Φ²

or

1.618… + 1 = 2.618…

 By applying the above Pythagorean equation to this, we can construct a right triangle, of sides a, b and c, or in this case a Golden Triangle of sides √Φ, 1 and Φ, which looks like this:

This creates a pyramid with a base width of 2 (i.e., two triangles above placed back-to-back) and a height of the square root of Phi, 1.272.  The ratio of the height to the base is 0.636.
According to Wikipedia, the Great Pyramid has a base of 230.4 meters (755.9 feet) and an estimated original height of 146.5 meters (480.6 feet).  This also creates a height to base ratio of 0.636, which indicates it is indeed a Golden Triangles, at least to within three significant decimal places of accuracy.  If the base is indeed exactly 230.4 meters then a perfect golden ratio would have a height of 146.53567, so the difference of only 0.3567 meters appears to be just a measurement or rounding difference.

The Great Pyramid has a surface ratio to base ratio of Phi, the Golden Ratio

A pyramid based on a golden triangle would have other interesting properties.  The surface area of the four sides would be a golden ratio of the surface area of the base.  The area of each trianglular side is the base x height / 2, or 2 x Φ/2 or Φ.  The surface area of the base is 2 x 2, or 4.  So four sides is 4 x Φ / 4, or Φ for the ratio of sides to base.

The Great Pyramid also has a relationship to Pi

There is another interesting aspect of this pyramid.  Construct a circle with a circumference of 8, the same as the perimeter of this pyramid with its base width of 2.  Then fold the arc of the semi-circle at a right angle, as illustrated below in “Revelation of the Pyramids”.  The height of the semi-circle will be the radius of the circle, which is 8/pi/2 or 1.273.

This is less than 1/10th of a percent different than the height of 1.272 computed above using the Golden Triangle.  Applying this to the 146.5 meter height of the pyramid would result in a difference in height between the two methods of only 0.14 meters (5.5 inches).

Its near perfect alignment to due north shows that little was left to chance

Some say that the relationships of the Great Pyramid’s dimensions to phi and pi either do not exist or happened by chance.  Would a civilization with the technological skill and knowledge to align the pyramid to within 1/15th of a degree to true north leave the dimensions of the pyramid to chance?  If they didn’t intend the precise 51.83 degree angle of a golden triangle, why would they have not used another simpler angle found in divisions of a circle such as 30, 45, 54 or 60 degrees?  If the dimensions of the pyramid were not based on both phi and pi, would it not be most reasonable to assume that phi was used since it is based on the visible base of the pyramid and not an invisible circle with the same circumference as that base?

Other possibilities for Phi and Pi relationships

Even if the Egyptians were using numbers that they understood to be the circumference of the circle to its diameter and the golden ratio that appeared in nature, it’s difficult to know if they truly understood the actual decimal representations of pi and phi as we understand them now. Since references to phi don’t appear in the historical record until the time of the Greeks hundreds of years later, some contend that the Egyptians did not have this knowledge and instead used integer approximations that achieved the same relationships and results in the design.
A rather amazing mathematical fact is that pi and the square root of phi can be approximated with a high degree of accuracy using simple integers. Pi can be approximated as 22/7, resulting in a repeating decimal number 3.142857142857… which is different from Pi by only 4/100′s of a percent. The square root of Phi can be approximatey by 14/11, resulting in a repeating decimal number 1.2727…, which is different from Phi by less than 6/100′s of a percent.  That means that Phi can be approximated as 256/121.
The Great Pyramid could thus have been based on 22/7 or 14/11 in the geometry shown about.  Even if the Egyptians only understood pi and/or phi through their integer approximations, the fact that the pyramid uses them shows that there was likely some understanding and intent of their mathematical importance in their application. It’s possible though that the pyramid dimensions could have been intended to represent only one of these numbers, either pi or phi, and the mathematics would have included the other automatically.  We really don’t know with certainty how the pyramid was designed as this knowledge could have existed and then been lost. The builders of such incredible architecture may have had far greater knowledge and sophistication than we may know, and it’s possible that both pi and phi as we understand them today could have been the driving factors in the design of the pyramid.

 

 

 

Does infinity exist?

by John D. Barrow

In the latest poll of our Science fiction, science fact project you told us that you wanted to know if infinity exists. Here is an answer, based on an interview with the cosmologist John D. Barrow. Clickhere to see other articles on infinity and here to listen to our interview with Barrow as a podcast.

Does infinity exist?

This is a surprisingly ancient question. It was Aristotle who first introduced a clear distinction to help make sense of it. He distinguished between two varieties of infinity. One of them he called a potential infinity: this is the type of infinity that characterises an unending Universe or an unending list, for example the natural numbers 1,2,3,4,5,..., which go on forever. These are lists or expanses that have no end or boundary: you can never reach the end of all numbers by listing them, or the end of an unending universe by travelling in a spaceship. Aristotle was quite happy about these potential infinities, he recognised that they existed and they didn't create any great scandal in his way of thinking about the Universe.

Aristotle distinguished potential infinities from what he calledactual infinities. These would be something you could measure, something local, for example the density of a solid, or the brightness of a light, or the temperature of an object, becoming infinite at a particular place or time. You would be able to encounter this infinity locally in the Universe. Aristotle banned actual infinities: he said they couldn't exist. This was bound up with his other belief, that there couldn't be a perfect vacuum in nature. If there could, he believed you would be able to push and accelerate an object to infinite speed because it would encounter no resistance.

For several thousands of years Aristotle's philosophy underpinned Western and Christian dogma and belief about the nature of the Universe. People continued to believe that actual infinities could not exist, in fact the only actual infinity that was supposed to exist was the divine.

Mathematical infinities

But in the world of mathematics things changed towards the end of the 19th century when the mathematician Georg Cantor developed a more subtle way of defining mathematical infinities. Cantor recognised that there was a smallest type of infinity: the unending list of natural numbers 1,2,3,4,5, ... . He called this a countable infinity. Any other infinity that could be counted by putting its members in one-to-one correspondence with the natural numbers was also called a countable infinity.

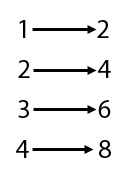The even numbers are in one-to-one correspondence with the natural numbers.

This idea had some funny consequences. For example, the list of all even numbers is also a countable infinity. Intuitively you might think there are only half as many even numbers as natural numbers because that would be true for a finite list. But when the list becomes unending that is no longer true. You can draw a line from 1 to 2 and from 2 to 4 and from 3 to 6 and so on forever in the two lists. Every even number will be joined to one and only one number in the list of natural numbers, so there are as many numbers in the one list as there are in the other. This fact was first noticed by Galileo (although he counted the squares 1, 4, 9, 16, ..., rather than the even numbers) who thought it was so strange that it put him off thinking about infinite collections of things any further. He thought there was just something dangerously paradoxical about them. For Cantor, though, this feature of being able to create a one-to-one correspondence between a set of numbers and a subset of them was the defining characteristic of an infinite set.

Similarly, the list of all the rational numbers, that is all the fractions, is a countable infinity. The way to count those systematically is to add the numerator and the denominator, and then first write down all the fractions for which this sum is 2 (there is only one, 1/1), then all the ones for which it is 3 (1/2 and 2/1), and so on. Each time you are counting only a finite number of fractions (the number of fractions p/q where p+q=n is n-1). This is an infallible recipe for counting all the rational numbers: you won't miss any. This shows that the rational numbers are countable too, even though in an intuitive sense there seem to be lots more of them than there are natural numbers.

Cantor then went on to show that there are also other types of infinity that are in some sense infinitely larger because they cannot be counted in this way. One such infinity is characterised by the list of all real numbers. These cannot be counted; there is no recipe for listing them systematically. This uncountable infinity is also called the continuum.

But finding this infinitely bigger set of the real numbers wasn't the end of the story. Cantor showed that you could find infinitely bigger sets still, all the way upwards forever: there was no biggest possible infinite collection of things. If someone presented you with an infinite set A, you could create a bigger one that wasn't in one-to-one correspondence with A just by finding the collection of all the possible subsets of A. This never-ending tower of infinities pointed towards something calledabsolute infinity — an unreachable summit of the tower of infinities. (You can find out more about Cantor's work in the Plus article A glimpse of Cantor's paradise.)

Mathematically, Cantor treated infinities not just as potential, but as actual. You could add them together — a countable infinity plus another countable infinity is a countable infinity — and so on. There was a great fuss in mathematics about whether this should be allowed. Some mathematicians thought that by allowing Cantor's transfinite quantities, as they were called, into mathematics, you were introducing some type of subtle contradiction somewhere. And if you introduce contradictions into a logical system, then eventually you will be able to prove that anything is true, so it would bring about the collapse of the whole system of mathematics.

This worry has led to the definition of finitist or constructivist mathematics, which only allows mathematical objects that you can construct by a finite sequence of logical arguments. Your mathematics then becomes a bit like what your computer can do. You set down certain axioms and only things that can be deduced from them by a finite sequence of logical steps are considered true. This means that you're not allowed to use proof by contradiction (or the law of the excluded middle) as an axiom, proposing that something does not exist and then deriving a contradiction from that proposition to conclude that it must exist. Nineteenth century proponents of this constructivist view were the Dutch mathematician LEJ Brouwer and Leopold Kroneker and in the twentieth centuryHermann Weyl was interested in it for a period. There are still some mathematicians who want to define mathematics in this way for philosophical reasons and others who are just interested in what you can prove if you do define it in this restricted way. (To find out more about this, read the Plusarticle Constructive maths.)

But generally Cantor's ideas have been accepted and today they form their own sub-branch of pure mathematics. This has led some philosophers, and even some theologians, to rethink their ancient attitudes to infinities. Because there are quite different varieties of infinity, it is clear that you don't have to regard the appearance of mathematical infinity as some sort of challenge to the divine as the medieval theologians believed. Cantor's ideas were at first actually taken up more enthusiastically by contemporay theologians than by mathematicians.

Scientists also started to distinguish between mathematical and physical infinities. In mathematics, if you say something "exists", what you mean is that it doesn't introduce a logical contradiction given a particular set of rules. But it doesn't mean that you can have one sitting on your desk or that there's one running around somewhere. Unicorns are not a logical impossibility but that doesn't mean that one exists biologically. When mathematicians demonstrated that non-Euclidean geometries can exist, they showed that there's an axiomatic system which permits them that is not self-contradictory. (You can find out more about non-Euclidean geometries in the article Strange geometries.)

Physical infinities

So infinities in modern physics have become separate from the study of infinities in mathematics. One area in physics where infinities are sometimes predicted to arise is aerodynamics or fluid mechanics. For example, you might have a wave becoming very, very steep and non-linear and then forming a shock. In the equations that describe the shock wave formation some quantities may become infinite. But when this happens you usually assume that it's just a failure of your model. You might have neglected to take account of friction or viscosity and once you include that into your equations the velocity gradient becomes finite — it might still be very steep, but the viscosity smoothes over the infinity in reality. In most areas of science, if you see an infinity, you assume that it's down to an inaccuracy or incompleteness of your model.

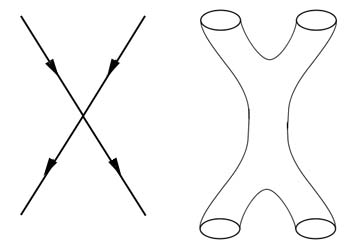
Two particles meeting form a sharp corner (left) but two loops coming together are like two pairs of trousers sown together. (The trouser diagram has time going downwards and space horizontal.)

In particle physics there has been a much longer-standing and more subtle problem. Quantum electrodynamics is the best theory in the whole of science, its predictions are more accurate than anything else that we know about the Universe. Yet extracting those predictions presented an awkward problem: when you did a calculation to see what you should observe in an experiment you always seemed to get an infinite answer with an extra finite bit added on. If you then subtracted off the infinity, the finite part that you were left with was the prediction you expected to see in the lab. And this always matched experiment fantastically accurately. This process of removing the infinities was calledrenormalisation. Many famous physicists found it deeply unsatisfactory. They thought it might just be a symptom of a theory that could be improved.

This is why string theory created great excitement in the 1980s and why it suddenly became investigated by a huge number of physicists. It was the first time that particle physicists found a finite theory, a theory which didn't have these infinities popping up. The way it did it was to replace the traditional notion that the most basic entities in the theory (for example photons or electrons) should be point-like objects that move through space and time and so trace out lines in spacetime. Instead, string theory considers the most basic entities to be lines, or little loops, which trace out tubes as they move. When you have two point-like particles moving through space and interacting, it's like two lines hitting one another and forming a sharp corner at the place where they meet. It's that sharp corner in the picture that's the source of the infinities in the description. But if you have two loops coming together, it's rather like two legs of a pair of trousers. Then two more loops move out from the interaction — that's like sewing another pair of trousers onto the first pair. What you get is a smooth transition. This was the reason why string theory was so appealing, it was the first finite theory of particle physics.

Cosmological infinities

Simulated view of a black hole. Image: Alain Riazuelo.

Another type of infinity arises in gravitation theory and cosmology. Einstein's theory of general relativity suggests that an expanding Universe (as we observe ours to be) started at a time in the finite past when its density was infinite — this is what we call the Big Bang. Einstein's theory also predicts that if you fell into a black hole, and there are many black holes in our Galaxy and nearby, you would encounter an infinite density at the centre. These infinities, if they do exist, would be actual infinities.

People's attitudes to these infinities differ. Cosmologists who come from particle physics and are interested in what string theory has to say about the beginning of the Universe would tend to the view that these infinities are not real, that they are just an artifact of the unfinished character of our theory. There are others, Roger Penrose is one for example, who think that that the initial infinity at the beginning of the Universe plays a very important role in the structure of physics. But even if these infinities are an artifact, the density still becomes stupefyingly high: 10⁹⁶ times bigger than that of water. For all practical purposes that's so high that we need a description of the effects of quantum theory on the character of space, time and gravity to understand what goes on there.

Something very odd can happen if we assume that our Universe will eventually stop expanding and contract back to another infinity, a big crunch. That big crunch could be non-simultaneous because some parts of the Universe, where there are galaxies and so on, are denser than others. The places that are denser will run into their future infinities before the low-density regions. If we were in a bit of the Universe that had a greatly delayed future infinity, or even none at all, then we could look back and see the end of the Universe happening in other places — we would see something infinite. You might see evidence of space and time coming to an end elsewhere.

But it's hard to predict exactly what you will see if an actual infinity arises somewhere. The way our Universe is set up at the moment, there is a curious defense mechanism. A simple interpretation of things suggests that there is an infinite density occurring at the centre of every black hole, which is just like the infinity at the end of the Universe. But a black hole creates a horizon around this phenomenon: not even light can escape from its vicinity. So we are insulated, we cannot see what goes on at those places where the density looks as though it's going to be infinite. And neither can the infinity influence us. These horizons protect us from the consequences of places where the density might be infinite and they stop us seeing what goes on there, unless of course we are inside a black hole.

Another question is whether our Universe is spatially finite or infinite. I think we can never know. It could be finite but of a size that is arbitrarily large. But to many people the idea of a finite Universe immediately raises the question of what is beyond. There is no beyond — the Universe is everything there is. To understand this, let's think of two-dimensional universes because they are easier to envisage. If we pick up a sheet of A4 paper we see that it has an edge, so how could it be that a finite Universe doesn't have an edge? But the point is that the piece of paper is flat. If we think of a closed 2D surface that's curved, like the surface of a sphere, then the area of the sphere is finite: you only need a finite amount of paint to paint it. But if you walk around on it, unlike with the flat piece of paper, you never encounter an edge. So curved spaces can be finite but have no boundary or edge.

To understand an expanding two-dimensional Universe, let's first think of the infinite case in which the Universe looks the same on average wherever you go. Then wherever you stand and look around you, it looks as though the Universe is expanding away from you at the centre because every place is like the centre. For a finite spherical universe, imagine the sphere as the balloon with the galaxies marked on the surface. When you start to inflate it the galaxies start to recede from one another. Wherever you stand on the surface of the balloon you would see all those other galaxies expanding away from you as the rubber expands. The centre of the expansion is not on the surface, it is in another dimension, in this case the 3rd dimension. So our three-dimensional Universe, if it is finite and positively curved, behaves as though it's the three-dimensional surface of an imaginary four-dimensional ball.

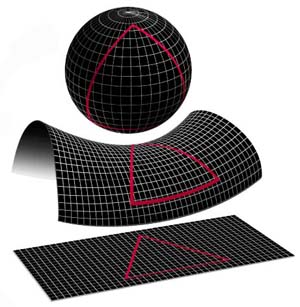
The sphere has positive curvature, the saddle has negative curvature and the flat plane has zero curvature. The triangles are formed by drawing the shortest lines between pairs of points. Where the sum of the angles exceeds (is less than) 180 degrees the surface has positive (negative) curvature. When it equals 180 degrees the surface is flat, with zero curvature. Image courtesy NASA.

Einstein told us that the geometry of space is determined by the density of material in it. Rather like a rubber trampoline: if you put material on the trampoline it deforms the curvature. If there is a lot of material in the space, it causes a huge depression and the space closes up. So a high density Universe requires a spherical geometry and it will have a finite volume. But if you have relatively little material present to deform space, you get a negatively curved space, shaped like a saddle or a potato crisp. Such a negatively curved space can continue to be stretched and expand forever. A low density Universe, if it has a simple geometry, will have an infinite size and volume. But if it has a more exotic topology, like a torus, it could also have a finite volume. One of the mysteries about Einstein's equations is that they tell you how you can work out the geometry from the distribution of matter, but his equations have nothing to say about the topology of the Universe. Maybe a deeper theory of quantum gravity will have something to say about that.

---

About the author

John D. Barrow is Professor of Mathematical Sciences at the University of Cambridge, author of many popular science books and director of the Millennium Mathematics Project of which Plus is a part.

Barrow is the author of The infinite book: A short guide to the boundless, timeless and endless, which tells you lots more about infinity. His Book of universes is also relevant to the last part of this article about cosmology and string theory. See the links below for both books.

Fuente: http://plus.maths.org/content/does-infinity-exist

Cuestionario sobre Infinitos

1) ¿Cuántas variedades de infinitos distinguió Aristóteles?

2) ¿Cómo se llama el tipo de infinito que desarrolló el matemático George Cantor ?

3) ¿Es un infinito contable el conjunto de los números racionales?

4) Encuentra un ejemplo de un infinito no contable.

5) ¿Cuáles fueron las consecuencias del nuevo concepto de infinito introducido por Cantor? ¿Fueron aceptadas sus ideas ?

6) Nombrar otros tipos de infinitos que no sean los infinitos matemáticos.

Video del Profesor ADRIAN PAENZA SOBRE EL INFINITO

Números Primos 

http://www.youtube.com/watch?v=qi6MBSjhsDg&feature=endscreen

The distribution of prime numbers is one of the most difficult questions in mathematics. There are ways to arrange prime numbers so that some interesting patterns emerge, but yet the actual distribution remains irrational and transcendental.

The first 10 seconds of this animation show over 13 thousands prime numbers arranged in circles of 720 slots each. Only the slots corresponding to prime numbers are filled in with black ink. The distribution is rather chaotic, although some radial lines could be seen.

The middle 10 seconds show the distributions of the cubes of the prime numbers. Every black dot is on the same circle, but its location along the circle is based on the 3-rd power of the number modulo 720. Obviously, the prime dots are grouped in several radial streams.

The final 10 seconds show the rather shocking distribution of the 12-th power of the primer numbers. It appears that except for the first three prime numbers, the 12-th power of all the rest land themselves on the same slot of each circle!

Thus, is p is a prime number greater than 5, then p^12=720n+1 for some integer n.

There is nothing magic in 720. If we choose 360 slots or even 144 we still get a similar result. For those of you, thinking about asking to see the distribution of the 13-th power ... the answer is disappointing. The 13-th power of primes are distributed quite chaotically. Sorry.

The music used in this animation is from "Nullsion" by Xelysion

http://www.artistserver.com/Xelysion

PRIMOSSOPA

Descubrir 5 palabras del lenguaje matemático presentes en el texto del Número Primo y en la siguiente sopa de letras: 

http://www.educaplay.com/es/recursoseducativos/1017831/numeros_primos.htm

PRIME NUMBER 

A prime number (or a prime) is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example, 5 is prime because only 1 and 5 evenly divide it, whereas 6 is composite because it has the divisors 2 and 3 in addition to 1 and 6. The fundamental theorem of arithmetic establishes the central role of primes in number theory: any integer greater than 1 can be expressed as a product of primes that is unique up to ordering. The uniqueness in this theorem requires excluding 1 as a prime because one can include arbitrarily-many instances of 1 in any factorization, e.g., 3, 1 × 3, 1 × 1 × 3, etc. are all valid factorizations of 3.

The property of being prime (or not) is called primality. A simple but slow method of verifying the primality of a given number n is known as trial division. It consists of testing whether n is a multiple of any integer between 2 and \sqrt{n}. Algorithms much more efficient than trial division have been devised to test the primality of large numbers. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. As of February 2013, the largest known prime number has 17,425,170 decimal digits.

There are infinitely many primes, as demonstrated by Euclid around 300 BC. There is no known useful formula that sets apart all of the prime numbers from composites. However, the distribution of primes, that is to say, the statistical behaviour of primes in the large, can be modelled. The first result in that direction is the prime number theorem, proven at the end of the 19th century, which says that the probability that a given, randomly chosen number n is prime is inversely proportional to its number of digits, or to the logarithm of n.

Many questions around prime numbers remain open, such as Goldbach's conjecture (that every even integer greater than 2 can be expressed as the sum of two primes), and the twin prime conjecture (that there are infinitely many pairs of primes whose difference is 2). Such questions spurred the development of various branches of number theory, focusing on analytic or algebraic aspects of numbers. Primes are used in several routines in information technology, such as public-key cryptography, which makes use of properties such as the difficulty of factoring large numbers into their prime factors. Prime numbers give rise to various generalizations in other mathematical domains, mainly algebra, such as prime elements and prime ideals.

http://en.wikipedia.org/wiki/Prime_number