Does infinity exist?
by John D. Barrow
In the latest poll of our Science fiction, science fact project you told us that you wanted to know if infinity exists. Here is an answer, based on an interview with the cosmologist John D. Barrow. Clickhere to see other articles on infinity and here to listen to our interview with Barrow as a podcast.
Does infinity exist?
This is a surprisingly ancient question. It was Aristotle who first introduced a clear distinction to help make sense of it. He distinguished between two varieties of infinity. One of them he called a potential infinity: this is the type of infinity that characterises an unending Universe or an unending list, for example the natural numbers 1,2,3,4,5,..., which go on forever. These are lists or expanses that have no end or boundary: you can never reach the end of all numbers by listing them, or the end of an unending universe by travelling in a spaceship. Aristotle was quite happy about these potential infinities, he recognised that they existed and they didn't create any great scandal in his way of thinking about the Universe.
Aristotle distinguished potential infinities from what he calledactual infinities. These would be something you could measure, something local, for example the density of a solid, or the brightness of a light, or the temperature of an object, becoming infinite at a particular place or time. You would be able to encounter this infinity locally in the Universe. Aristotle banned actual infinities: he said they couldn't exist. This was bound up with his other belief, that there couldn't be a perfect vacuum in nature. If there could, he believed you would be able to push and accelerate an object to infinite speed because it would encounter no resistance.
For several thousands of years Aristotle's philosophy underpinned Western and Christian dogma and belief about the nature of the Universe. People continued to believe that actual infinities could not exist, in fact the only actual infinity that was supposed to exist was the divine.
Mathematical infinities
But in the world of mathematics things changed towards the end of the 19th century when the mathematician Georg Cantor developed a more subtle way of defining mathematical infinities. Cantor recognised that there was a smallest type of infinity: the unending list of natural numbers 1,2,3,4,5, ... . He called this a countable infinity. Any other infinity that could be counted by putting its members in one-to-one correspondence with the natural numbers was also called a countable infinity.
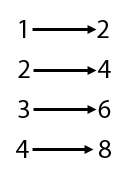The even numbers are in one-to-one correspondence with the natural numbers.
This idea had some funny consequences. For example, the list of all even numbers is also a countable infinity. Intuitively you might think there are only half as many even numbers as natural numbers because that would be true for a finite list. But when the list becomes unending that is no longer true. You can draw a line from 1 to 2 and from 2 to 4 and from 3 to 6 and so on forever in the two lists. Every even number will be joined to one and only one number in the list of natural numbers, so there are as many numbers in the one list as there are in the other. This fact was first noticed by Galileo (although he counted the squares 1, 4, 9, 16, ..., rather than the even numbers) who thought it was so strange that it put him off thinking about infinite collections of things any further. He thought there was just something dangerously paradoxical about them. For Cantor, though, this feature of being able to create a one-to-one correspondence between a set of numbers and a subset of them was the defining characteristic of an infinite set.
Similarly, the list of all the rational numbers, that is all the fractions, is a countable infinity. The way to count those systematically is to add the numerator and the denominator, and then first write down all the fractions for which this sum is 2 (there is only one, 1/1), then all the ones for which it is 3 (1/2 and 2/1), and so on. Each time you are counting only a finite number of fractions (the number of fractions p/q where p+q=n is n-1). This is an infallible recipe for counting all the rational numbers: you won't miss any. This shows that the rational numbers are countable too, even though in an intuitive sense there seem to be lots more of them than there are natural numbers.
Cantor then went on to show that there are also other types of infinity that are in some sense infinitely larger because they cannot be counted in this way. One such infinity is characterised by the list of all real numbers. These cannot be counted; there is no recipe for listing them systematically. This uncountable infinity is also called the continuum.
But finding this infinitely bigger set of the real numbers wasn't the end of the story. Cantor showed that you could find infinitely bigger sets still, all the way upwards forever: there was no biggest possible infinite collection of things. If someone presented you with an infinite set A, you could create a bigger one that wasn't in one-to-one correspondence with A just by finding the collection of all the possible subsets of A. This never-ending tower of infinities pointed towards something calledabsolute infinity — an unreachable summit of the tower of infinities. (You can find out more about Cantor's work in the Plus article A glimpse of Cantor's paradise.)
Mathematically, Cantor treated infinities not just as potential, but as actual. You could add them together — a countable infinity plus another countable infinity is a countable infinity — and so on. There was a great fuss in mathematics about whether this should be allowed. Some mathematicians thought that by allowing Cantor's transfinite quantities, as they were called, into mathematics, you were introducing some type of subtle contradiction somewhere. And if you introduce contradictions into a logical system, then eventually you will be able to prove that anything is true, so it would bring about the collapse of the whole system of mathematics.
This worry has led to the definition of finitist or constructivist mathematics, which only allows mathematical objects that you can construct by a finite sequence of logical arguments. Your mathematics then becomes a bit like what your computer can do. You set down certain axioms and only things that can be deduced from them by a finite sequence of logical steps are considered true. This means that you're not allowed to use proof by contradiction (or the law of the excluded middle) as an axiom, proposing that something does not exist and then deriving a contradiction from that proposition to conclude that it must exist. Nineteenth century proponents of this constructivist view were the Dutch mathematician LEJ Brouwer and Leopold Kroneker and in the twentieth centuryHermann Weyl was interested in it for a period. There are still some mathematicians who want to define mathematics in this way for philosophical reasons and others who are just interested in what you can prove if you do define it in this restricted way. (To find out more about this, read the Plusarticle Constructive maths.)
But generally Cantor's ideas have been accepted and today they form their own sub-branch of pure mathematics. This has led some philosophers, and even some theologians, to rethink their ancient attitudes to infinities. Because there are quite different varieties of infinity, it is clear that you don't have to regard the appearance of mathematical infinity as some sort of challenge to the divine as the medieval theologians believed. Cantor's ideas were at first actually taken up more enthusiastically by contemporay theologians than by mathematicians.
Scientists also started to distinguish between mathematical and physical infinities. In mathematics, if you say something "exists", what you mean is that it doesn't introduce a logical contradiction given a particular set of rules. But it doesn't mean that you can have one sitting on your desk or that there's one running around somewhere. Unicorns are not a logical impossibility but that doesn't mean that one exists biologically. When mathematicians demonstrated that non-Euclidean geometries can exist, they showed that there's an axiomatic system which permits them that is not self-contradictory. (You can find out more about non-Euclidean geometries in the article Strange geometries.)
Physical infinities
So infinities in modern physics have become separate from the study of infinities in mathematics. One area in physics where infinities are sometimes predicted to arise is aerodynamics or fluid mechanics. For example, you might have a wave becoming very, very steep and non-linear and then forming a shock. In the equations that describe the shock wave formation some quantities may become infinite. But when this happens you usually assume that it's just a failure of your model. You might have neglected to take account of friction or viscosity and once you include that into your equations the velocity gradient becomes finite — it might still be very steep, but the viscosity smoothes over the infinity in reality. In most areas of science, if you see an infinity, you assume that it's down to an inaccuracy or incompleteness of your model.
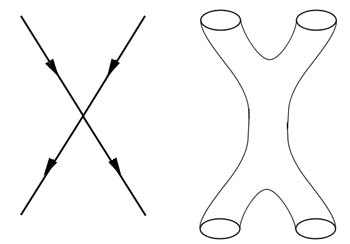
Two particles meeting form a sharp corner (left) but two loops coming together are like two pairs of trousers sown together. (The trouser diagram has time going downwards and space horizontal.)
In particle physics there has been a much longer-standing and more subtle problem. Quantum electrodynamics is the best theory in the whole of science, its predictions are more accurate than anything else that we know about the Universe. Yet extracting those predictions presented an awkward problem: when you did a calculation to see what you should observe in an experiment you always seemed to get an infinite answer with an extra finite bit added on. If you then subtracted off the infinity, the finite part that you were left with was the prediction you expected to see in the lab. And this always matched experiment fantastically accurately. This process of removing the infinities was calledrenormalisation. Many famous physicists found it deeply unsatisfactory. They thought it might just be a symptom of a theory that could be improved.
This is why string theory created great excitement in the 1980s and why it suddenly became investigated by a huge number of physicists. It was the first time that particle physicists found a finite theory, a theory which didn't have these infinities popping up. The way it did it was to replace the traditional notion that the most basic entities in the theory (for example photons or electrons) should be point-like objects that move through space and time and so trace out lines in spacetime. Instead, string theory considers the most basic entities to be lines, or little loops, which trace out tubes as they move. When you have two point-like particles moving through space and interacting, it's like two lines hitting one another and forming a sharp corner at the place where they meet. It's that sharp corner in the picture that's the source of the infinities in the description. But if you have two loops coming together, it's rather like two legs of a pair of trousers. Then two more loops move out from the interaction — that's like sewing another pair of trousers onto the first pair. What you get is a smooth transition. This was the reason why string theory was so appealing, it was the first finite theory of particle physics.
Cosmological infinities
Simulated view of a black hole. Image: Alain Riazuelo.
Another type of infinity arises in gravitation theory and cosmology. Einstein's theory of general relativity suggests that an expanding Universe (as we observe ours to be) started at a time in the finite past when its density was infinite — this is what we call the Big Bang. Einstein's theory also predicts that if you fell into a black hole, and there are many black holes in our Galaxy and nearby, you would encounter an infinite density at the centre. These infinities, if they do exist, would be actual infinities.
People's attitudes to these infinities differ. Cosmologists who come from particle physics and are interested in what string theory has to say about the beginning of the Universe would tend to the view that these infinities are not real, that they are just an artifact of the unfinished character of our theory. There are others, Roger Penrose is one for example, who think that that the initial infinity at the beginning of the Universe plays a very important role in the structure of physics. But even if these infinities are an artifact, the density still becomes stupefyingly high: 1096 times bigger than that of water. For all practical purposes that's so high that we need a description of the effects of quantum theory on the character of space, time and gravity to understand what goes on there.
Something very odd can happen if we assume that our Universe will eventually stop expanding and contract back to another infinity, a big crunch. That big crunch could be non-simultaneous because some parts of the Universe, where there are galaxies and so on, are denser than others. The places that are denser will run into their future infinities before the low-density regions. If we were in a bit of the Universe that had a greatly delayed future infinity, or even none at all, then we could look back and see the end of the Universe happening in other places — we would see something infinite. You might see evidence of space and time coming to an end elsewhere.
But it's hard to predict exactly what you will see if an actual infinity arises somewhere. The way our Universe is set up at the moment, there is a curious defense mechanism. A simple interpretation of things suggests that there is an infinite density occurring at the centre of every black hole, which is just like the infinity at the end of the Universe. But a black hole creates a horizon around this phenomenon: not even light can escape from its vicinity. So we are insulated, we cannot see what goes on at those places where the density looks as though it's going to be infinite. And neither can the infinity influence us. These horizons protect us from the consequences of places where the density might be infinite and they stop us seeing what goes on there, unless of course we are inside a black hole.
Another question is whether our Universe is spatially finite or infinite. I think we can never know. It could be finite but of a size that is arbitrarily large. But to many people the idea of a finite Universe immediately raises the question of what is beyond. There is no beyond — the Universe is everything there is. To understand this, let's think of two-dimensional universes because they are easier to envisage. If we pick up a sheet of A4 paper we see that it has an edge, so how could it be that a finite Universe doesn't have an edge? But the point is that the piece of paper is flat. If we think of a closed 2D surface that's curved, like the surface of a sphere, then the area of the sphere is finite: you only need a finite amount of paint to paint it. But if you walk around on it, unlike with the flat piece of paper, you never encounter an edge. So curved spaces can be finite but have no boundary or edge.
To understand an expanding two-dimensional Universe, let's first think of the infinite case in which the Universe looks the same on average wherever you go. Then wherever you stand and look around you, it looks as though the Universe is expanding away from you at the centre because every place is like the centre. For a finite spherical universe, imagine the sphere as the balloon with the galaxies marked on the surface. When you start to inflate it the galaxies start to recede from one another. Wherever you stand on the surface of the balloon you would see all those other galaxies expanding away from you as the rubber expands. The centre of the expansion is not on the surface, it is in another dimension, in this case the 3rd dimension. So our three-dimensional Universe, if it is finite and positively curved, behaves as though it's the three-dimensional surface of an imaginary four-dimensional ball.
The sphere has positive curvature, the saddle has negative curvature and the flat plane has zero curvature. The triangles are formed by drawing the shortest lines between pairs of points. Where the sum of the angles exceeds (is less than) 180 degrees the surface has positive (negative) curvature. When it equals 180 degrees the surface is flat, with zero curvature. Image courtesy NASA.
Einstein told us that the geometry of space is determined by the density of material in it. Rather like a rubber trampoline: if you put material on the trampoline it deforms the curvature. If there is a lot of material in the space, it causes a huge depression and the space closes up. So a high density Universe requires a spherical geometry and it will have a finite volume. But if you have relatively little material present to deform space, you get a negatively curved space, shaped like a saddle or a potato crisp. Such a negatively curved space can continue to be stretched and expand forever. A low density Universe, if it has a simple geometry, will have an infinite size and volume. But if it has a more exotic topology, like a torus, it could also have a finite volume. One of the mysteries about Einstein's equations is that they tell you how you can work out the geometry from the distribution of matter, but his equations have nothing to say about the topology of the Universe. Maybe a deeper theory of quantum gravity will have something to say about that.
About the author
John D. Barrow is Professor of Mathematical Sciences at the University of Cambridge, author of many popular science books and director of the Millennium Mathematics Project of which Plus is a part.
Barrow is the author of The infinite book: A short guide to the boundless, timeless and endless, which tells you lots more about infinity. His Book of universes is also relevant to the last part of this article about cosmology and string theory. See the links below for both books.
Cuestionario sobre Infinitos
1) ¿Cuántas variedades de infinitos distinguió Aristóteles?
2) ¿Cómo se llama el tipo de infinito que desarrolló el matemático George Cantor ?
3) ¿Es un infinito contable el conjunto de los números racionales?
4) Encuentra un ejemplo de un infinito no contable.
5) ¿Cuáles fueron las consecuencias del nuevo concepto de infinito introducido por Cantor? ¿Fueron aceptadas sus ideas ?
6) Nombrar otros tipos de infinitos que no sean los infinitos matemáticos.
Video del Profesor ADRIAN PAENZA SOBRE EL INFINITO
Los conjuntos numéricos son conjuntos cuyos elementos son exclusivamente números y que tienen en común una serie de propiedades. Por ejemplo el sistema más usual en aritmética natural está formado por el conjunto de los números naturales, con la suma, la multiplicación y las relaciones usuales de orden aditivo.
![[HOME]](file:///C:/DOCUME~1/NOEMIG~1/CONFIG~1/Temp/msohtmlclip1/01/clip_image001.gif){kind=small}
